Mint Banjo

About

Squarejam is a unique block-moving puzzle game for mobile, built in the Unity game engine. The best introduction is to watch this short trailer:

Where to play

You can play squarejam on android via the app store: squarejam

You can also play the game on itch.io: https://mintbanjo.itch.io/squarejam

How to play

• Swap colours on the grid boundary. Each square rotates to face their corresponding colour.
• Press the tick to take a move. Each square teleports in the direction it is facing.
• Two squares can’t teleport to the same space.
• Squares can’t leave the grid.
• Reach the circular goal with a matching square to clear the level!

Levels increase in difficulty and quickly become quite tricky. Earn star-ratings by finding the fastest route on each level. An example level completion is show below.

Development

Squarejam was developed using the Unity game engine, and coded using the C# programming language.

Level design

Levels in squarejam have various degrees of difficulty, ranging from easy to very hard. Levels are created by placing an initial configuration of coloured blocks, and the goal, in various positions. There is a huge number of possible levels. An example level looks like this:

When designing levels, we need to know the following:

• Is the level solvable?
• What is the optimal solution? (fewest number of moves to reach the goal)
• How difficult is the level?

It is challenging, time consuming and error-prone to answer those questions manually. There is probably an analytic solution on the “solvability” of a given level, but it is likely a very challenging topic in pure math theory. For now, a brute force “squarejam solver” was developed in C++.

Designing such a solver is not trivial, as the number of possible paths to check quickly becomes quite large as the number of moves increases. The player chooses a move by arranging the four coloured sides into desired positions. Therefore, there are 4 factorial choices for each move = 24 choices. If we want to look for a solution up to move 10, that is 24^10 = 63,403,380,965,376 possible moves.

The solver traverses the tree of all possible board states up to a chosen maximum moves depth. We start by choosing a move from the set of possible moves, applying the move to the current state, and testing the new state for a solution. We repeat this process, testing each new move until we reach the maximum number of moves. Then we head back down the tree, testing each move we missed at each tree depth.

There are some shortcuts we can take to reduce the total number of examined states, and speed up the program:

• Is the current state legal?
• Is the current state identical to a previous state from this path?
• Calculate the minimum distance to the goal – is it still possible to reach the goal before the maximum move count?
• If we already found a solution, is it still possible for this path to be a faster solution?

If any test fails, we can abandon the current path and save millions of state checks.

In addition to finding the fastest solution (if one exists), the solver can provide other diagnostic information about the level, which can help quantify how difficult a level is. This allows us to arrange to levels in ascending order of difficulty to better improve the user experience.

We can apply the solver to the example level above, and it outputs a solution:

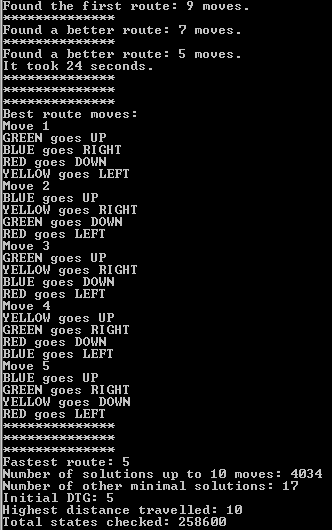
We chose to find all solutions up to move 10, rather than stop when a single fastest solution was found, so it took 24 seconds it total to solve the level. We find that the initial minimum distance of a red square to the red goal was 5, and that the fastest route was 5 moves. That is, there were no counter-intuitive, planning-type moves to make: it is possible to head directly to the goal. Already, this tells us the level is somewhat easier than other existing levels. Move instructions for an optimal solution are also printed.

We also know there are 4034 total solutions up to 10 moves, and that there are 17 other solutions which can reach the goal in 5 moves. Also, the total number of states checked was 258,600.

We can use these numbers to rank the levels in difficulty, and judge how fun a level will be. If there are very few states checked, it can be quite frustrating for the player, as there are very few legal moves to make: the level becomes an exercise in trial and error, rather than perception and logic. We want a level to have high square manoeuvrability, but a low number of solutions.

Very difficult levels have a higher number of moves than the initial distance to goal. For example, the hardest level has an initial distance of 6, but requires 12 moves to solve. That is, the player cannot make a beeline straight for the goal: they must spend additional moves merely shuffling the squares around and planning ahead to find a solution.